300. 最长递增子序列 ​

题目地址

动态规划 ​

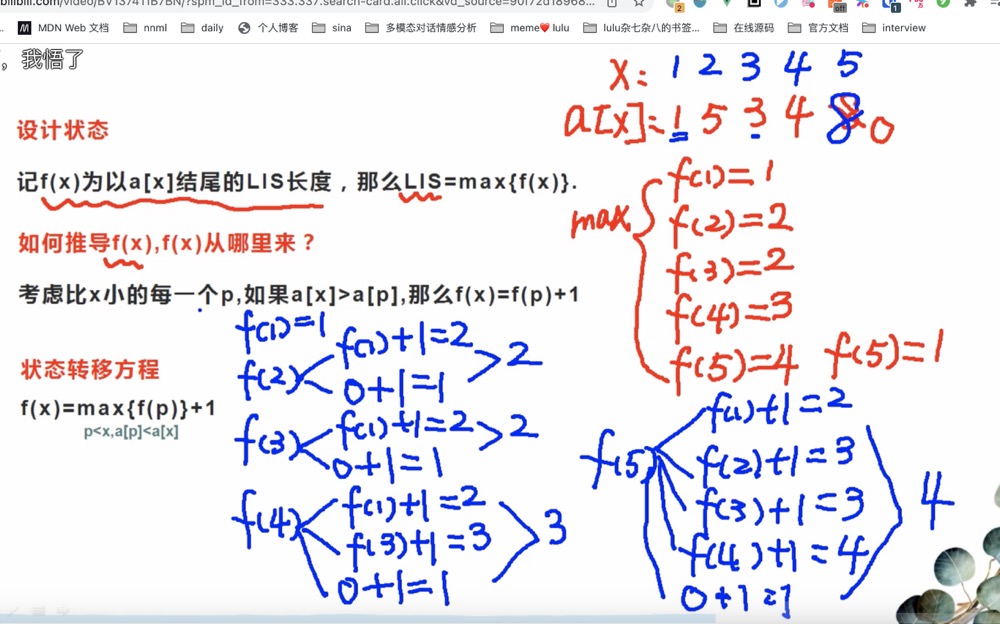
1、5、2、4、7

f[i] => i 是下标 f[i] 代表以 nums[i] 为结尾的最大子序列

• f(0) => [1] => 1
• f(1) => [1、5] => 2
• f(2) => [1、2] or [1、5] => 2
• f(3) => [1、2、4] => 3
• f(4) => [1、2、4、7] => 4

所以最大是 4

规律：

f(0) = 1;

• f(0) + 1 max = 1
• 0 + 1

f(2)

• f(0) + 1 max = 2
• 0 + 1

f(3) =

• f(0) + 1
• f(2) + 1 max = 3
• 0 + 1

f(4)

• f(0) + 1
• f(2) + 1
• f(3) + 1 max = 4
• 0 + 1

动态规划 + 二分查找 ​

TODO