堆排序

大顶堆
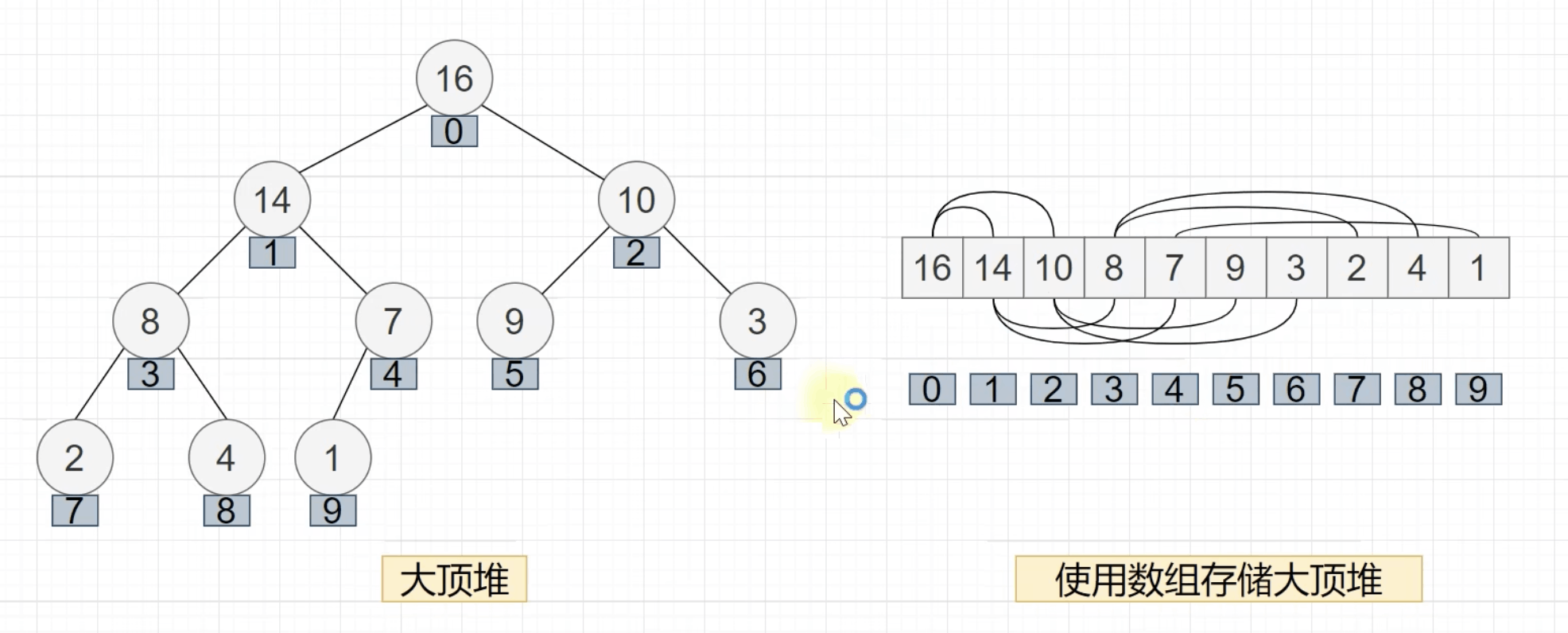
下标为 i 的节点:
- 其父节点的坐标为
(i - 1) >> 1 - 左孩子
i * 2 + 1 - 右孩子
i * 2 + 2
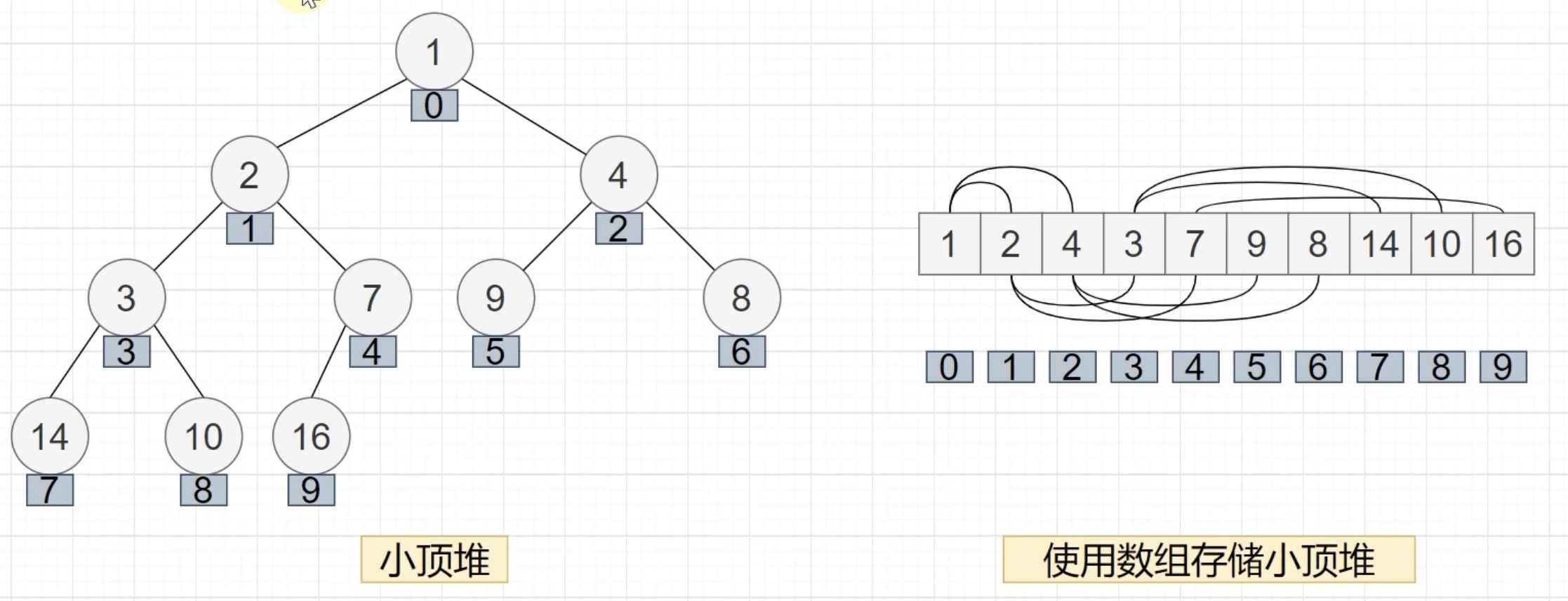
小顶堆
js
Array.prototype.heapSort = function () {
const arr = this;
let len = arr.length;
function swap(a, b) {
const tmp = arr[a];
arr[a] = arr[b];
arr[b] = tmp;
}
/**
* 维护堆的性质
* @param {number} i 当前在维护第几个节点
*/
function heap(i) {
let maxIndex = i;
let lIndex = i * 2 + 1;
let rIndex = i * 2 + 2;
// 找到 [当前节点 i, 左节点 lIndex,右节点 rIndex] 中最大的
if (lIndex < len && arr[lIndex] < arr[maxIndex]) {
maxIndex = lIndex;
}
if (rIndex < len && arr[rIndex] < arr[maxIndex]) {
maxIndex = rIndex;
}
// 如果不满足堆堆性质(孩子节点存在大于父节点的),执行交换,同时递归的维护后面的节点
if (i !== maxIndex) {
swap(i, maxIndex);
heap(maxIndex);
}
}
/**
* 建堆的过程需要从最后一个非叶子节点开始,逐个向前调用 heap 方法维护堆的性质
* 最后一个叶子节点的下标为 `len - 1`,它的父节点的下标为 `(len - 1 - 1) / 2`
*/
function buildHeap() {
for (let i = (len - 1 - 1) >> 1; i >= 0; i--) {
heap(i);
}
}
buildHeap();
console.log(arr);
for (let i = len - 1; i > 0; i--) {
swap(0, i);
len--;
heap(0);
}
console.log(arr);
}; limy-blog
limy-blog